FIR Filters Explained

Introduction

FIR filters have become increasingly popular in pro-audio in recent years. This has partly been driven by the availability of more powerful DSPs which are able to process multiple FIR filters in real-time. However, whilst FIR filters are a powerful tool they are also frequently misunderstood. This article will try (without going into the mathematical complexities) to explain what FIR filters are, as well their benefits and drawbacks compared to other filter types.

Back to Basics

To help us in our explanation, we’ll firstly consider an analogue 24dB/Octave Linkwitz low-pass filter with the following frequency response :

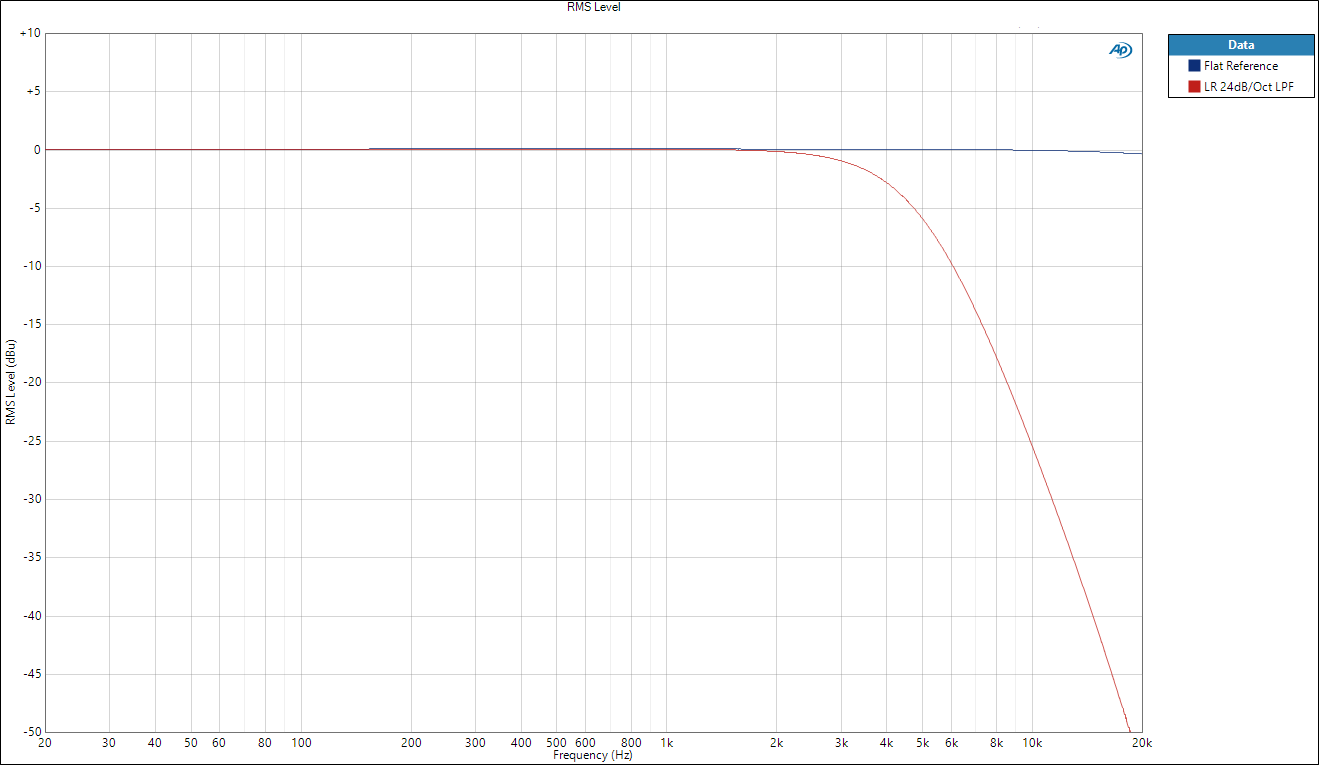
As well as the frequency response of this filter, the other important behaviour in audio systems is the phase response :

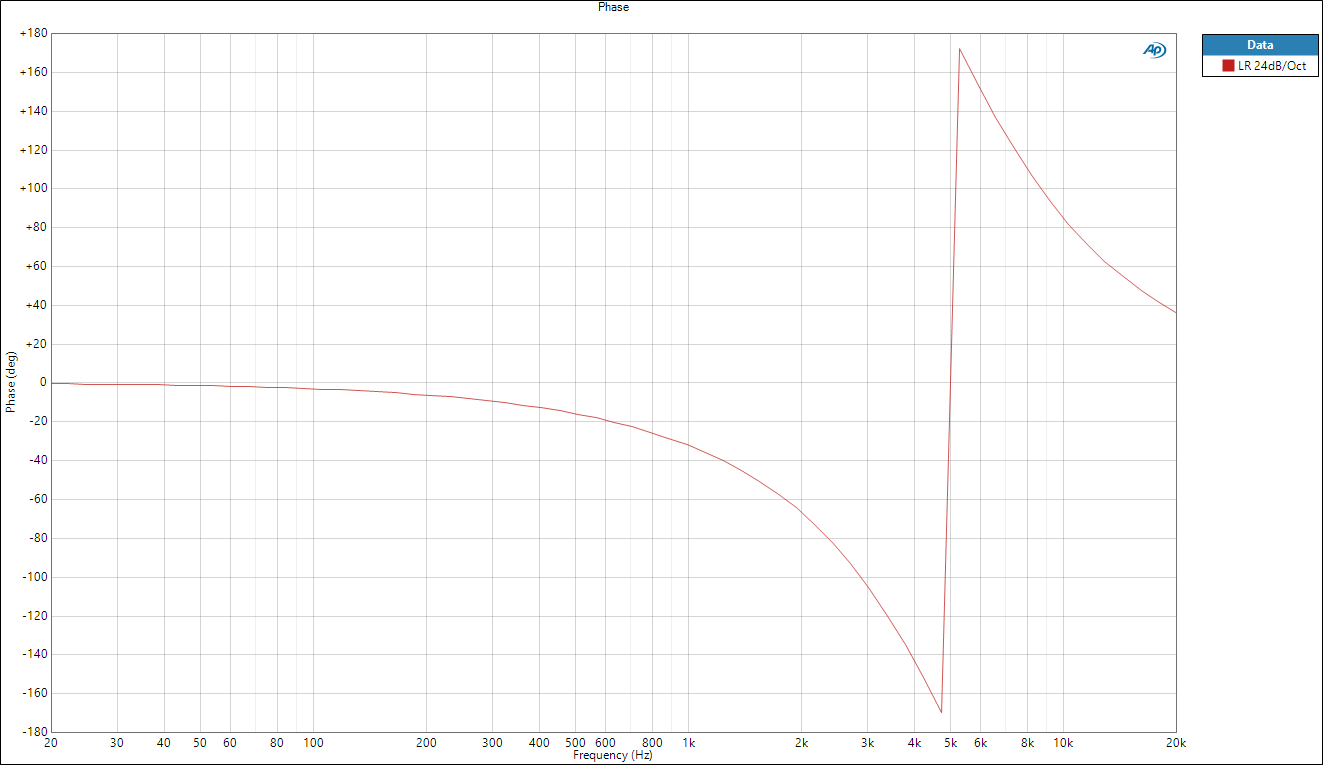
The phase response curve of the filter describes a frequency-dependent delay that the filter adds to the signal. So we can see that as well as altering the response of the system in the frequency domain, the filter also alters the system in the time-domain. Normally this isn’t a problem, but it’s something that loudspeaker designers spend a great deal of time optimising in multi-way systems. These phase shifts can have significant effects on the interaction of loudspeaker drivers in different frequency bands near the crossover points as well as the polar response of the loudspeaker.

Digital Equivalents

In a DSP we can produce digital filters which behave almost identically to their analogue equivalents. The most common way to do this is by using a DSP algorithm known as a “biquad” to design IIR filters. We won’t go into detail here about the details of IIR filter design, as the maths gets complex quite quickly. To summarise their operation simply, IIR filters feed part of the previous input and output samples back in to the filter at different gain levels to create the next sample output, creating a feedback cycle which will theoretically go on forever. This continuous feedback system is why this type of digital filter is called Infinite Impulse Response (IIR).

IIR Advantages

IIR filters have been the standard filter method in digital audio for over 20 years and have some distinct advantages :

– Almost identical behaviour to the analogue equivalents (which eased the transition from analogue to digital)
– Computationally efficient using biquads (important in the early days of DSP when there was little processing power available)

IIR Limitations

Despite their widespread use, the design of IIR filters is quite mathematically complex. However, in pro-audio DSP systems this complexity is hidden from the user – just enter the parameters to define the filter shape and the software calculates the coefficients needed to ensure the filter behaves as expected and stays stable. Despite their advantages and widespread use, IIR filters have some limitations :

– Design of asymmetric filters, or filters with a complex frequency response is difficult
– Difficult to control phase response of filters

Time Domain

Traditional audio engineering has focused on the frequency domain, especially obtaining a “flat” frequency response. But in loudspeaker design and multi-way loudspeaker systems, we also need to consider the effect in the time domain due to filtering. By combining the frequency and phase responses of a system, we can mathematically apply an Inverse Fourier Transform to get the impulse response of a system. Put simply, this is the output of the system over time if you put a single impulse into the system. The impulse response of an IIR implementation of a Linkwitz Riley 24dB/octave low-pass filter would look like this :

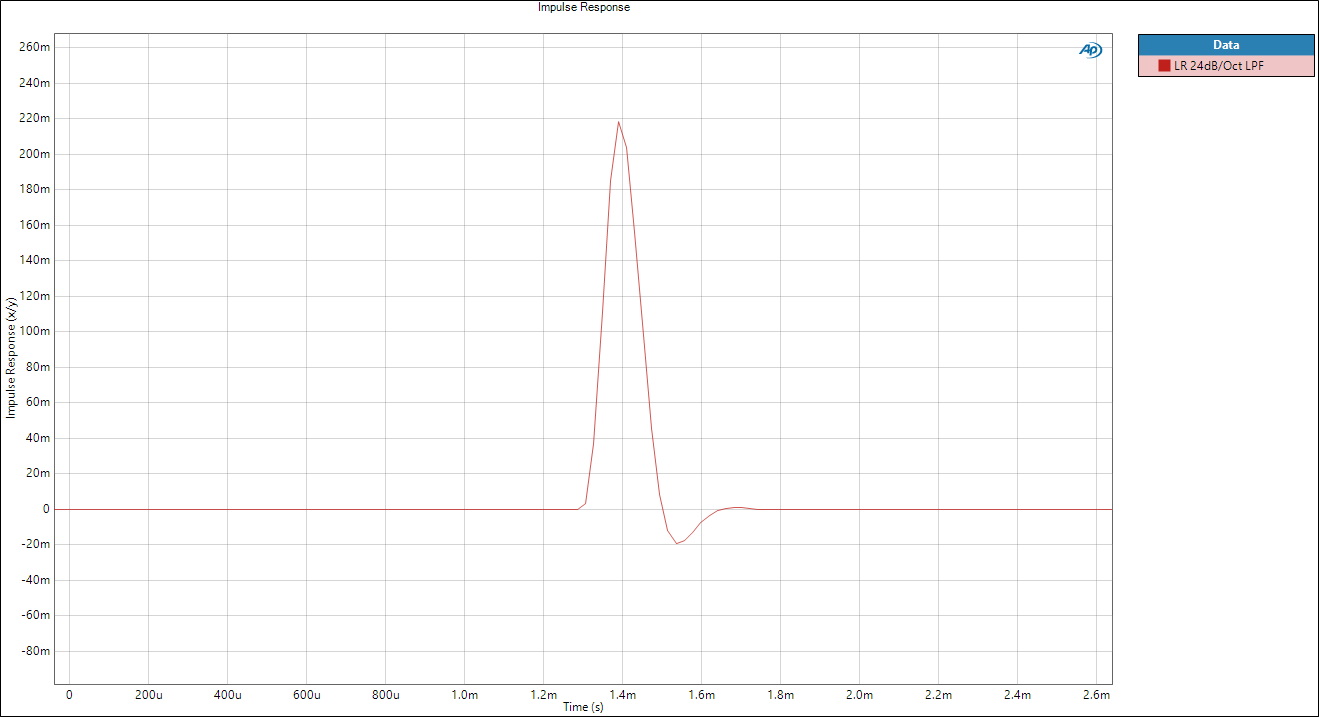
The problem with the impulse response is that when we look at it, it’s not very easy to understand what effect it will have on a signal. This is one reason why we tend to focus mainly on the frequency response and phase response, which are mathematically equivalent but provide more useful information. However, there are characteristics of the impulse response which have important implications, as we’ll discuss later.

FIR Filters

The alternative to IIR filters is the FIR filter which, as the name suggests, are designed using a fixed length impulse response. Actually, the normal design method for FIR filters is to design the frequency and phase response, then calculate an inverse Fourier transform to generate the impulse response (which is the FIR filter itself). From a design point of view, this has many advantages as it allows the design of filters with complex frequency responses without any of the side-effects of a non-linear phase response to cause problems in the acoustic system.

FIR Advantages

– Can create filters with arbitrary frequency response
– Have control over the phase response of the filter

FIR Example

So we can design a 24dB/octave low-pass filter with (almost) exactly the same frequency response as our Linkwitz Riley filter as before :

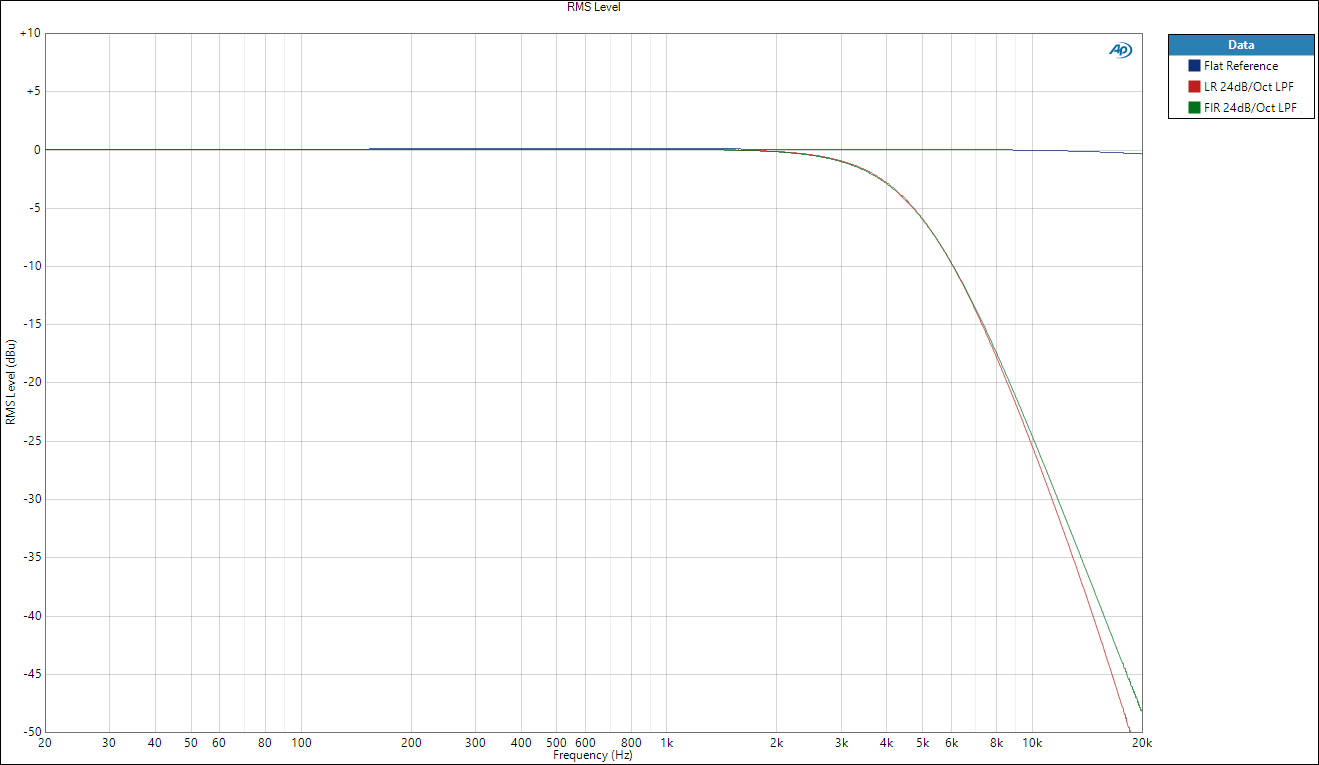
This filter has been measured using a 1024 tap FIR filter at 96kHz designed in rePhase, loaded into an NST D48S. This version of the filter has a completely flat phase response (compared against the IIR version for reference) :

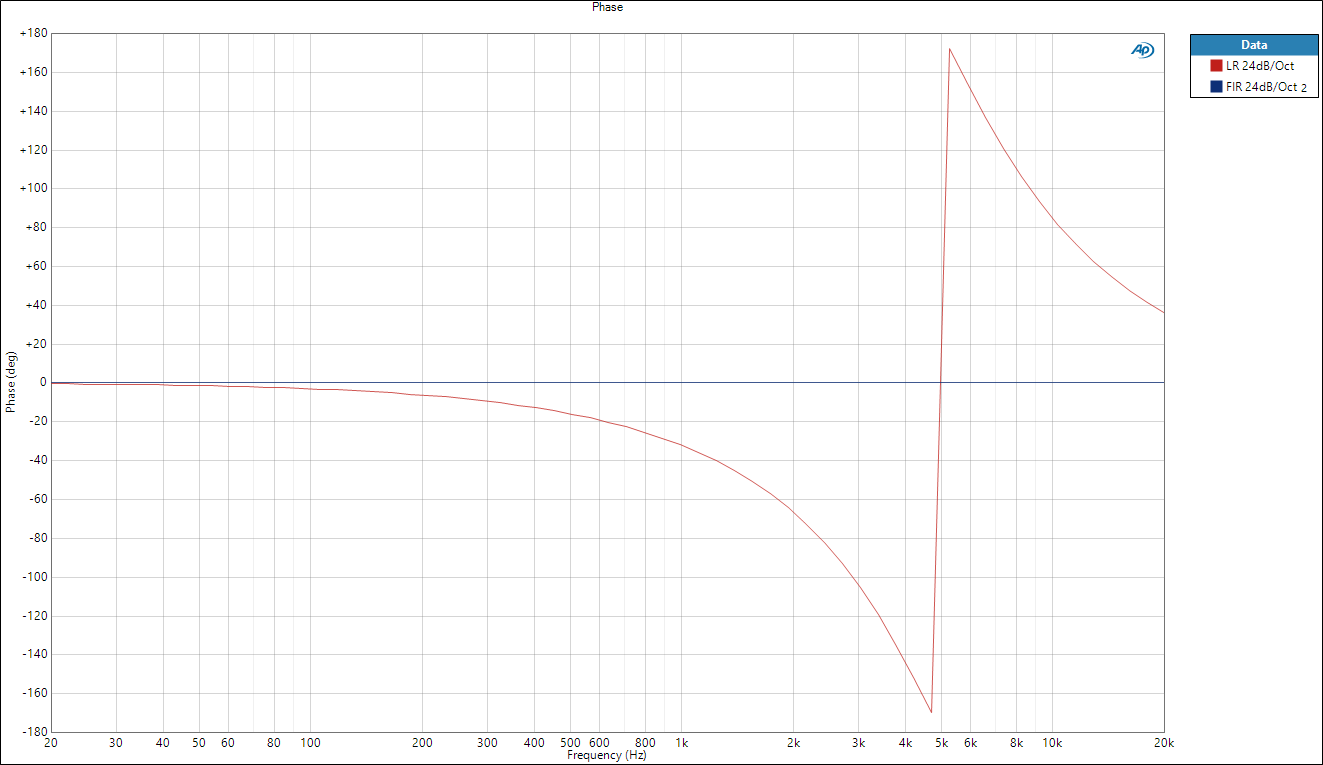
However, we also need to look at the impulse response of our filter :

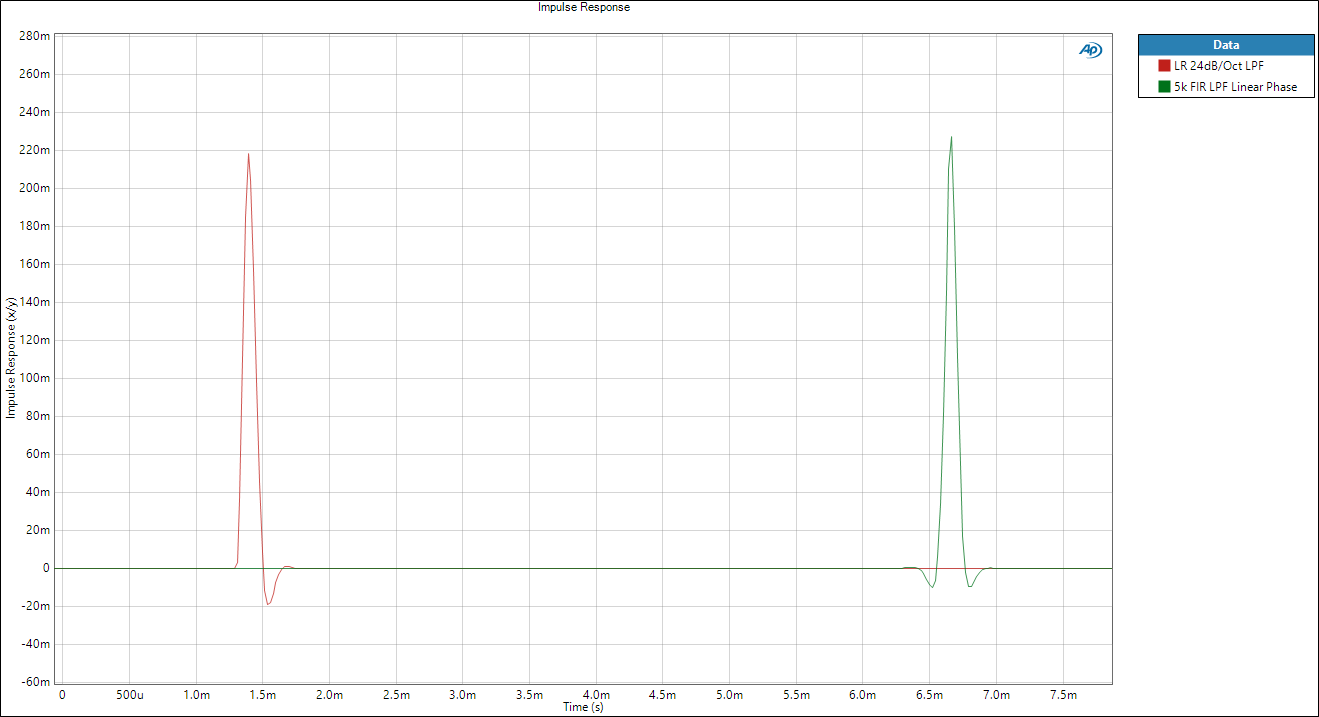
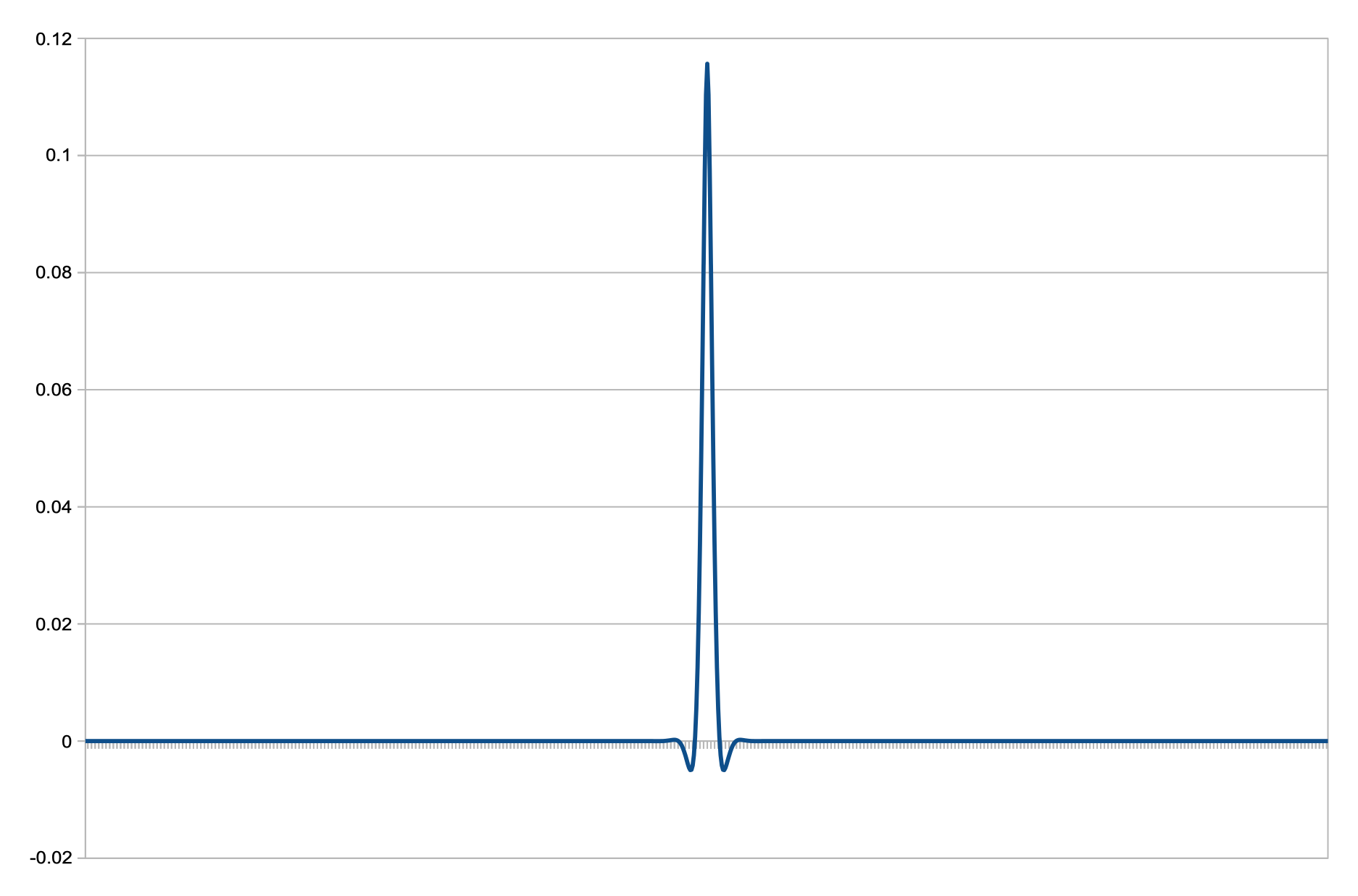
The measurements of both the FIR and IIR are shown here so we can see that it takes over 5ms longer for the impulse to come out of the FIR filter compared to our IIR filter with the same frequency response. This length of time is determined by the length of the FIR filter, or the number of “taps”. In this case, the impulse response is exactly what we expect because it’s the same as we designed in rePhase :

This long “group delay”, the overall delay to the signal, is the price that we pay for a flat phase response. In fact it is the mechanism required to create the flat phase response. In some applications, a large group delay in the system isn’t a problem but in real-time applications like live sound or gaming, it’s a major consideration.

There is one other feature of these impulse responses worth noting. The IIR filter impulse response is asymmetric, and is characterised by a single large peak (in response to the impulse input), followed by a decay which determines the behaviour of the filter. But for an FIR filter with linear phase response the impulse response is always symmetrical about the large peak (the position of which determines the group delay of the filter). This means that the filter starts generating audible output for several cycles before the main peak of the impulse has passed through the filter, creating a kind of “pre-ringing” on transients which in some circumstances can sound a little odd.

FIR Limitations

So although we get some very desirable advantages using FIR filters, there are still disadvantages :

– Long group delay compared to IIR filters
– Require significantly more DSP power than a similar EQ/crossover in IIR filters
– Group delay length proportional to lowest frequency affected by the filter
– Only work over a limited frequency range for a given filter length
– Poor frequency resolution at lower frequencies

Conclusions

Both IIR and FIR filtering techniques have applications in pro-audio, but care must be taken when choosing which is best suited for a particular application as both methods have benefits and drawbacks. There is sometimes a perception that FIR filters are superior, mainly because of the control they give over the phase response. While there are many powerful advantages to FIR filters, this functionality comes at a cost, not only in terms of group delay, but also the restriction of the frequency range which can be controlled.

Further Reading

This article has focused on the concepts of FIR and IIR filters, rather than the engineering and mathematical details. The following links contain some more technical detail on FIR filters :

An FIR tutorial on the Eclipse Audio site
Part 1 of a ProSoundWeb article on FIR Filters
Part 2 of a ProSoundWeb article on FIR Filters